 Ilustrasi(Pinterest)
Ilustrasi(Pinterest)
Dalam dunia matematika, bangun datar memegang peranan krusial sebagai fondasi untuk memahami konsep geometri yang lebih kompleks. Setiap bangun datar memiliki karakteristik unik yang membedakannya satu sama lain. Pemahaman mendalam mengenai sifat-sifat ini esensial, bukan hanya bagi pelajar, tetapi juga bagi para profesional di berbagai bidang seperti arsitektur, desain, dan teknik.
Memahami Esensi Bangun Datar
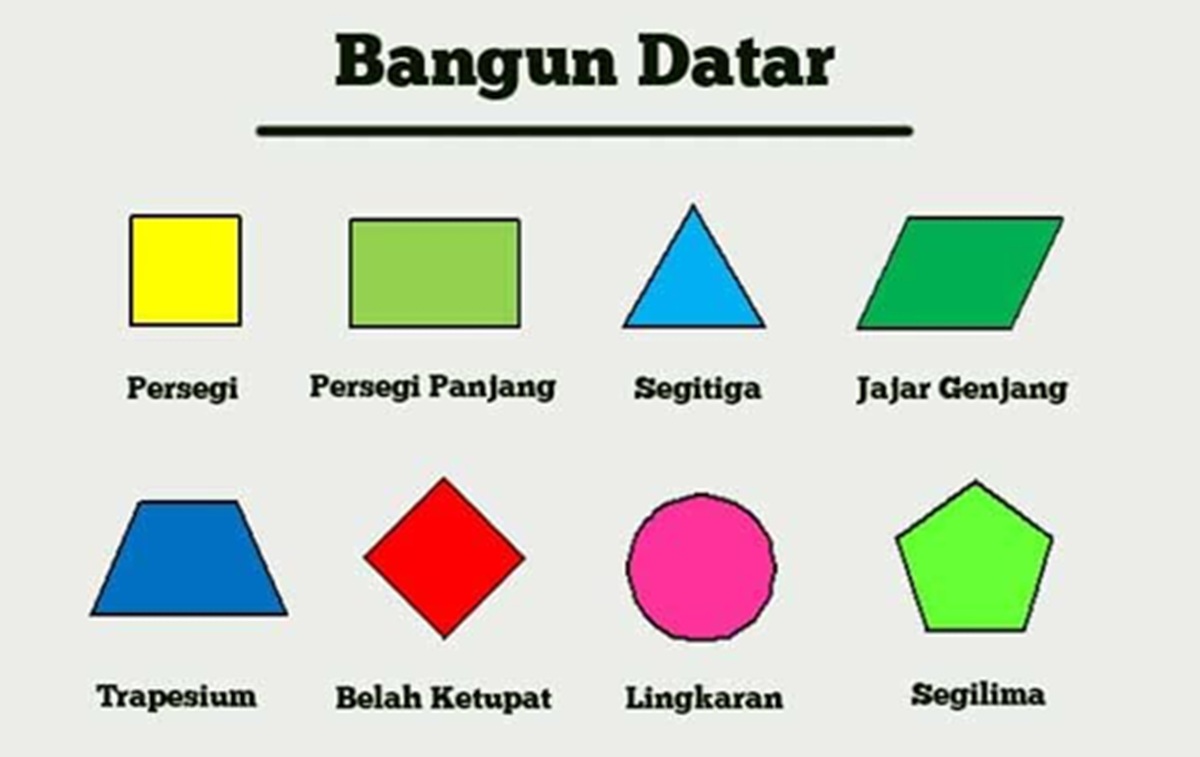
Bangun datar, secara sederhana, adalah objek geometri dua dimensi yang hanya memiliki panjang dan lebar. Mereka terdefinisi oleh garis-garis yang membentuk sisi-sisinya dan titik-titik yang menjadi sudutnya. Keragaman bangun datar sangatlah luas, mulai dari bentuk-bentuk sederhana seperti segitiga dan persegi, hingga bentuk yang lebih kompleks seperti trapesium dan lingkaran. Setiap bentuk memiliki formula khusus untuk menghitung luas dan kelilingnya, yang menjadi dasar dalam berbagai aplikasi praktis.
Segitiga: Bangun datar yang paling mendasar, dibentuk oleh tiga sisi dan tiga sudut. Jumlah ketiga sudutnya selalu 180 derajat. Segitiga dapat diklasifikasikan berdasarkan panjang sisinya (sama sisi, sama kaki, sembarang) dan berdasarkan besar sudutnya (lancip, tumpul, siku-siku).
Persegi: Bangun datar segi empat yang memiliki empat sisi sama panjang dan empat sudut siku-siku (90 derajat). Persegi merupakan bentuk yang sangat simetris dan sering digunakan dalam desain karena kemudahannya dalam perhitungan dan konstruksi.
Lingkaran: Bangun datar yang dibentuk oleh kumpulan titik-titik yang berjarak sama dari satu titik pusat. Jarak tersebut disebut jari-jari lingkaran. Lingkaran tidak memiliki sudut atau sisi lurus, melainkan garis lengkung yang sempurna.
Persegi Panjang: Bangun datar segi empat yang memiliki dua pasang sisi sejajar yang sama panjang dan empat sudut siku-siku. Berbeda dengan persegi, sisi-sisi persegi panjang tidak harus sama panjang.
Trapesium: Bangun datar segi empat yang memiliki sepasang sisi sejajar. Sisi yang sejajar disebut alas, sedangkan sisi yang tidak sejajar disebut kaki. Trapesium memiliki berbagai jenis, seperti trapesium sama kaki dan trapesium siku-siku.
Jajar Genjang: Bangun datar segi empat yang memiliki dua pasang sisi sejajar. Sudut-sudut yang berhadapan pada jajar genjang sama besar.
Belah Ketupat: Bangun datar segi empat yang memiliki empat sisi sama panjang. Sudut-sudut yang berhadapan pada belah ketupat sama besar, dan diagonal-diagonalnya saling berpotongan tegak lurus.
Layang-layang: Bangun datar segi empat yang memiliki dua pasang sisi yang berdekatan sama panjang. Diagonal-diagonal layang-layang saling berpotongan tegak lurus, dan salah satu diagonalnya membagi diagonal lainnya menjadi dua bagian sama panjang.
Sifat-Sifat Utama Bangun Datar
Setiap bangun datar memiliki serangkaian sifat yang mendefinisikannya. Sifat-sifat ini mencakup panjang sisi, besar sudut, simetri, dan hubungan antara elemen-elemennya. Memahami sifat-sifat ini memungkinkan kita untuk mengidentifikasi, mengklasifikasikan, dan menganalisis bangun datar secara efektif.
Panjang Sisi: Panjang sisi merupakan salah satu karakteristik paling dasar dari bangun datar. Pada beberapa bangun datar, seperti persegi dan belah ketupat, semua sisi memiliki panjang yang sama. Pada bangun datar lain, seperti persegi panjang dan trapesium, sisi-sisi memiliki panjang yang berbeda.
Besar Sudut: Besar sudut adalah ukuran rotasi antara dua sisi yang bertemu pada suatu titik. Sudut diukur dalam derajat. Pada beberapa bangun datar, seperti persegi dan persegi panjang, semua sudut adalah sudut siku-siku (90 derajat). Pada bangun datar lain, sudut-sudut dapat memiliki ukuran yang berbeda.
Simetri: Simetri adalah sifat suatu bangun datar yang tetap tidak berubah setelah mengalami transformasi tertentu, seperti refleksi atau rotasi. Beberapa bangun datar, seperti persegi dan lingkaran, memiliki simetri yang tinggi. Bangun datar lain, seperti segitiga sembarang, mungkin tidak memiliki simetri sama sekali.
Luas: Luas adalah ukuran seberapa besar permukaan yang ditutupi oleh suatu bangun datar. Luas diukur dalam satuan persegi, seperti sentimeter persegi (cm²) atau meter persegi (m²). Setiap bangun datar memiliki rumus khusus untuk menghitung luasnya.
Keliling: Keliling adalah panjang total sisi-sisi suatu bangun datar. Keliling diukur dalam satuan panjang, seperti sentimeter (cm) atau meter (m). Untuk menghitung keliling suatu bangun datar, kita cukup menjumlahkan panjang semua sisinya.
Diagonal: Diagonal adalah garis yang menghubungkan dua sudut yang tidak berdekatan pada suatu bangun datar. Beberapa bangun datar, seperti persegi dan persegi panjang, memiliki dua diagonal. Diagonal dapat digunakan untuk menghitung luas dan sifat-sifat lainnya dari bangun datar.
Aplikasi Praktis Sifat-Sifat Bangun Datar
Pemahaman tentang sifat-sifat bangun datar memiliki aplikasi yang luas dalam berbagai bidang. Dalam arsitektur, pengetahuan tentang geometri digunakan untuk merancang bangunan yang stabil dan estetis. Dalam desain, bangun datar digunakan untuk menciptakan pola dan komposisi visual yang menarik. Dalam teknik, sifat-sifat bangun datar digunakan untuk menghitung kekuatan dan stabilitas struktur.
Arsitektur: Arsitek menggunakan prinsip-prinsip geometri untuk merancang bangunan yang aman, fungsional, dan indah. Mereka mempertimbangkan bentuk, ukuran, dan proporsi bangunan untuk menciptakan ruang yang nyaman dan efisien. Misalnya, penggunaan segitiga dalam struktur atap memberikan kekuatan dan stabilitas yang lebih besar.
Desain: Desainer menggunakan bangun datar untuk menciptakan pola, tekstur, dan komposisi visual yang menarik. Mereka mempertimbangkan hubungan antara berbagai bentuk dan warna untuk menciptakan desain yang harmonis dan efektif. Misalnya, penggunaan lingkaran dalam logo dapat memberikan kesan kelembutan dan kesatuan.
Teknik: Insinyur menggunakan sifat-sifat bangun datar untuk menghitung kekuatan dan stabilitas struktur. Mereka mempertimbangkan beban yang akan ditanggung oleh struktur dan memilih bahan dan desain yang sesuai untuk memastikan keamanan dan keandalan. Misalnya, penggunaan balok persegi panjang dalam jembatan memberikan kekuatan dan ketahanan terhadap lentur.
Matematika dan Pendidikan: Pemahaman tentang bangun datar adalah fondasi penting dalam pembelajaran matematika. Konsep-konsep seperti luas, keliling, dan simetri dipelajari melalui eksplorasi bangun datar. Ini membantu siswa mengembangkan kemampuan berpikir logis dan pemecahan masalah.
Seni dan Kerajinan: Bangun datar sering digunakan dalam seni dan kerajinan untuk menciptakan berbagai karya yang indah dan kreatif. Misalnya, dalam seni mozaik, potongan-potongan kecil bangun datar disusun untuk membentuk gambar yang lebih besar. Dalam kerajinan tangan, bangun datar dapat digunakan untuk membuat berbagai macam dekorasi dan perhiasan.
Rumus-Rumus Penting Bangun Datar
Berikut adalah beberapa rumus penting yang digunakan untuk menghitung luas dan keliling berbagai bangun datar:
| Segitiga | 1/2 x alas x tinggi | Jumlah panjang semua sisi |
| Persegi | sisi x sisi | 4 x sisi |
| Lingkaran | π x jari-jari² | 2 x π x jari-jari |
| Persegi Panjang | panjang x lebar | 2 x (panjang + lebar) |
| Trapesium | 1/2 x (jumlah sisi sejajar) x tinggi | Jumlah panjang semua sisi |
| Jajar Genjang | alas x tinggi | 2 x (alas + sisi miring) |
| Belah Ketupat | 1/2 x diagonal 1 x diagonal 2 | 4 x sisi |
| Layang-layang | 1/2 x diagonal 1 x diagonal 2 | 2 x (sisi pendek + sisi panjang) |
Catatan: π (pi) adalah konstanta matematika yang nilainya kira-kira 3.14159.
Tips dan Trik dalam Mempelajari Bangun Datar
Mempelajari bangun datar bisa menjadi lebih mudah dan menyenangkan dengan beberapa tips dan trik berikut:
Visualisasikan: Cobalah untuk membayangkan bangun datar dalam pikiran Anda. Gambarlah di atas kertas atau gunakan aplikasi komputer untuk membantu Anda memvisualisasikannya.
Gunakan Benda Nyata: Carilah benda-benda di sekitar Anda yang berbentuk bangun datar. Misalnya, ubin lantai berbentuk persegi, piring berbentuk lingkaran, dan atap rumah berbentuk segitiga.
Latihan Soal: Kerjakan soal-soal latihan untuk menguji pemahaman Anda tentang sifat-sifat bangun datar dan rumus-rumusnya.
Gunakan Sumber Belajar yang Beragam: Bacalah buku, artikel, dan tonton video tentang bangun datar. Gunakan sumber belajar yang sesuai dengan gaya belajar Anda.
Berkolaborasi dengan Teman: Belajarlah bersama teman-teman Anda. Diskusikan konsep-konsep yang sulit dan saling membantu dalam mengerjakan soal-soal latihan.
Manfaatkan Teknologi: Gunakan aplikasi dan perangkat lunak geometri untuk memvisualisasikan bangun datar dan melakukan perhitungan dengan mudah.
Kesimpulan
Bangun datar adalah elemen fundamental dalam geometri yang memiliki sifat-sifat unik dan aplikasi yang luas. Pemahaman mendalam tentang sifat-sifat ini sangat penting bagi siapa saja yang ingin menguasai konsep geometri dan menerapkannya dalam berbagai bidang. Dengan mempelajari sifat-sifat bangun datar, kita dapat mengembangkan kemampuan berpikir logis, pemecahan masalah, dan kreativitas. Dari arsitektur hingga desain, dari teknik hingga seni, bangun datar memainkan peran penting dalam membentuk dunia di sekitar kita. Oleh karena itu, mari terus eksplorasi dan mendalami keindahan dan kekuatan geometri bangun datar.
Dengan penguasaan konsep bangun datar, kita tidak hanya memahami matematika secara teoritis, tetapi juga mampu mengaplikasikannya dalam kehidupan sehari-hari. Kemampuan ini sangat berharga dalam menghadapi tantangan dan menciptakan solusi inovatif di berbagai bidang. Jadi, teruslah belajar dan eksplorasi dunia geometri yang menakjubkan ini!
Selain itu, penting untuk diingat bahwa pembelajaran bangun datar tidak hanya terbatas pada menghafal rumus dan definisi. Lebih dari itu, pembelajaran ini melibatkan pengembangan intuisi geometris, yaitu kemampuan untuk memahami dan memvisualisasikan hubungan spasial. Intuisi geometris ini sangat penting dalam memecahkan masalah-masalah kompleks yang melibatkan bentuk dan ruang.
Oleh karena itu, jangan hanya fokus pada menghafal rumus, tetapi juga berusahalah untuk mengembangkan intuisi geometris Anda. Latihlah kemampuan Anda untuk memvisualisasikan bangun datar dalam berbagai posisi dan orientasi. Eksperimen dengan berbagai transformasi geometris, seperti rotasi, refleksi, dan translasi. Dengan melatih intuisi geometris Anda, Anda akan menjadi lebih mahir dalam memahami dan memanipulasi bangun datar.
Terakhir, ingatlah bahwa pembelajaran adalah proses yang berkelanjutan. Jangan pernah berhenti belajar dan mengeksplorasi hal-hal baru. Dunia geometri sangat luas dan penuh dengan keajaiban yang menunggu untuk ditemukan. Dengan semangat belajar yang tinggi, Anda akan mampu menguasai konsep-konsep geometri yang lebih kompleks dan menerapkannya dalam berbagai bidang kehidupan. (Z-2)