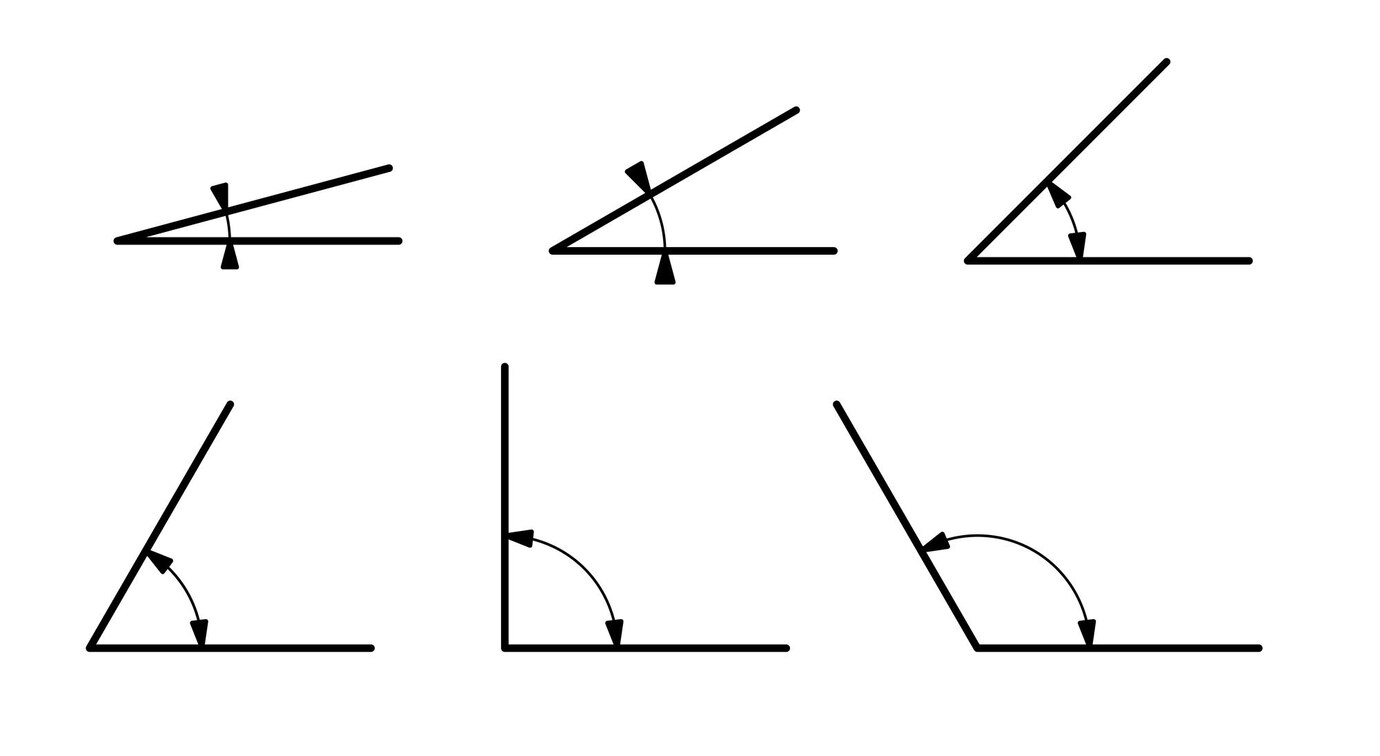Jenis-Jenis Sudut: Memahami Geometri Dasar

Ilustrasi(freepik.com)

DALAM dunia matematika, khususnya geometri, sudut memegang peranan krusial sebagai fondasi untuk memahami bentuk dan ruang. Sudut, secara sederhana, adalah ruang yang terbentuk antara dua garis yang bertemu pada satu titik yang disebut titik sudut. Pemahaman mendalam tentang berbagai jenis sudut membuka pintu menuju pemecahan masalah geometri yang kompleks dan aplikasi praktis dalam kehidupan sehari-hari, mulai dari arsitektur hingga navigasi.

Mengenal Lebih Dekat Klasifikasi Sudut

Sudut diklasifikasikan berdasarkan ukurannya, yang diukur dalam derajat (°). Setiap jenis sudut memiliki karakteristik unik yang membedakannya dari yang lain. Mari kita telaah berbagai jenis sudut dan sifat-sifatnya:

1. Sudut Lancip: Sudut lancip adalah sudut yang ukurannya lebih besar dari 0° tetapi kurang dari 90°. Bentuknya yang lancip membuatnya mudah dikenali. Contoh sudut lancip dapat ditemukan pada ujung pensil yang baru diraut atau pada irisan kue.

2. Sudut Siku-Siku: Sudut siku-siku adalah sudut yang ukurannya tepat 90°. Sudut ini sering dilambangkan dengan simbol kotak kecil di titik sudutnya. Sudut siku-siku sangat penting dalam konstruksi dan desain, karena memberikan kestabilan dan keseimbangan. Contoh sudut siku-siku dapat ditemukan pada sudut ruangan, bingkai jendela, atau buku.

3. Sudut Tumpul: Sudut tumpul adalah sudut yang ukurannya lebih besar dari 90° tetapi kurang dari 180°. Bentuknya yang tumpul membuatnya terlihat lebih lebar dari sudut siku-siku. Contoh sudut tumpul dapat ditemukan pada posisi jarum jam saat menunjukkan pukul 2 atau 4.

4. Sudut Lurus: Sudut lurus adalah sudut yang ukurannya tepat 180°. Sudut ini membentuk garis lurus. Contoh sudut lurus dapat ditemukan pada jalan yang lurus atau pada posisi jarum jam saat menunjukkan pukul 6.

5. Sudut Refleks: Sudut refleks adalah sudut yang ukurannya lebih besar dari 180° tetapi kurang dari 360°. Sudut ini memantul melewati garis lurus. Contoh sudut refleks lebih sulit ditemukan dalam kehidupan sehari-hari, tetapi dapat dibayangkan sebagai putaran yang hampir lengkap.

6. Sudut Penuh: Sudut penuh adalah sudut yang ukurannya tepat 360°. Sudut ini membentuk lingkaran penuh. Contoh sudut penuh dapat ditemukan pada putaran roda atau jarum jam setelah 12 jam.

Hubungan Antar Sudut: Lebih dari Sekadar Ukuran

Selain klasifikasi berdasarkan ukuran, sudut juga dapat dikelompokkan berdasarkan hubungannya dengan sudut lain. Beberapa hubungan antar sudut yang penting meliputi:

1. Sudut Berpenyiku (Complementary Angles): Dua sudut dikatakan berpenyiku jika jumlah ukurannya adalah 90°. Jika satu sudut berukuran 30°, maka sudut penyikunya berukuran 60°.

2. Sudut Berpelurus (Supplementary Angles): Dua sudut dikatakan berpelurus jika jumlah ukurannya adalah 180°. Jika satu sudut berukuran 120°, maka sudut pelurusnya berukuran 60°.

3. Sudut Bertolak Belakang (Vertical Angles): Sudut bertolak belakang terbentuk ketika dua garis berpotongan. Sudut-sudut yang saling berhadapan di titik potong tersebut memiliki ukuran yang sama.

4. Sudut Sehadap (Corresponding Angles): Sudut sehadap terbentuk ketika sebuah garis melintang memotong dua garis sejajar. Sudut-sudut yang berada pada posisi yang sama relatif terhadap garis melintang dan garis sejajar memiliki ukuran yang sama.

5. Sudut Dalam Berseberangan (Alternate Interior Angles): Sudut dalam berseberangan terbentuk ketika sebuah garis melintang memotong dua garis sejajar. Sudut-sudut yang berada di antara dua garis sejajar dan berseberangan terhadap garis melintang memiliki ukuran yang sama.

6. Sudut Luar Berseberangan (Alternate Exterior Angles): Sudut luar berseberangan terbentuk ketika sebuah garis melintang memotong dua garis sejajar. Sudut-sudut yang berada di luar dua garis sejajar dan berseberangan terhadap garis melintang memiliki ukuran yang sama.

Aplikasi Sudut dalam Kehidupan Sehari-hari

Pemahaman tentang jenis-jenis sudut dan hubungannya tidak hanya relevan dalam konteks akademis, tetapi juga memiliki aplikasi praktis yang luas dalam berbagai bidang kehidupan. Berikut adalah beberapa contohnya:

1. Arsitektur dan Konstruksi: Sudut memainkan peran penting dalam desain dan konstruksi bangunan. Sudut siku-siku digunakan untuk memastikan dinding tegak lurus dan bangunan stabil. Sudut-sudut lain digunakan untuk menciptakan desain yang estetis dan fungsional. Perhitungan sudut yang tepat sangat penting untuk memastikan kekuatan dan keamanan struktur.

2. Navigasi: Dalam navigasi, sudut digunakan untuk menentukan arah dan posisi. Kompas menggunakan sudut untuk menunjukkan arah mata angin. Pilot dan pelaut menggunakan sudut untuk menghitung jalur penerbangan dan pelayaran.

3. Teknik: Dalam bidang teknik, sudut digunakan dalam desain mesin dan peralatan. Sudut kemiringan, sudut potong, dan sudut gesek adalah beberapa contoh sudut yang penting dalam teknik mesin. Pemahaman tentang sudut juga penting dalam teknik sipil untuk desain jembatan, jalan, dan bendungan.

4. Seni dan Desain: Sudut digunakan dalam seni dan desain untuk menciptakan perspektif, keseimbangan, dan harmoni visual. Sudut pandang, sudut pencahayaan, dan sudut komposisi adalah beberapa contoh sudut yang penting dalam seni dan desain.

5. Olahraga: Dalam olahraga, sudut digunakan untuk menganalisis gerakan dan meningkatkan performa. Sudut lemparan, sudut tendangan, dan sudut ayunan adalah beberapa contoh sudut yang penting dalam olahraga.

Mengukur Sudut: Alat dan Teknik

Untuk mengukur sudut, kita menggunakan alat yang disebut busur derajat (protractor). Busur derajat adalah alat berbentuk setengah lingkaran yang memiliki skala dari 0° hingga 180°. Untuk mengukur sudut, kita letakkan titik tengah busur derajat pada titik sudut, lalu sejajarkan salah satu sisi sudut dengan garis 0° pada busur derajat. Ukuran sudut dapat dibaca pada skala busur derajat di mana sisi sudut yang lain berada.

Selain busur derajat, terdapat juga alat yang lebih canggih untuk mengukur sudut, seperti teodolit dan total station. Alat-alat ini digunakan dalam survei dan konstruksi untuk mengukur sudut dengan akurasi yang tinggi.

Tips dan Trik dalam Memahami Sudut

Berikut adalah beberapa tips dan trik yang dapat membantu Anda dalam memahami dan mengingat berbagai jenis sudut:

1. Visualisasi: Bayangkan berbagai jenis sudut dalam pikiran Anda. Gunakan benda-benda di sekitar Anda sebagai contoh sudut. Misalnya, sudut ruangan adalah sudut siku-siku, sedangkan ujung gunting adalah sudut lancip.

2. Asosiasi: Kaitkan setiap jenis sudut dengan kata kunci atau gambar yang mudah diingat. Misalnya, sudut lancip dapat diasosiasikan dengan lancip atau tajam, sedangkan sudut tumpul dapat diasosiasikan dengan tumpul atau lebar.

3. Latihan: Latih kemampuan Anda dalam mengidentifikasi dan mengukur sudut dengan mengerjakan soal-soal latihan. Semakin banyak Anda berlatih, semakin mudah Anda memahami konsep sudut.

4. Gunakan Alat Bantu: Manfaatkan alat bantu seperti busur derajat, penggaris, dan kertas berpetak untuk membantu Anda dalam menggambar dan mengukur sudut.

5. Cari Sumber Belajar Tambahan: Jika Anda masih kesulitan memahami konsep sudut, jangan ragu untuk mencari sumber belajar tambahan seperti buku, artikel, video, atau tutor.

Sudut dalam Trigonometri: Memperluas Pemahaman

Pemahaman tentang sudut menjadi semakin penting dalam trigonometri, cabang matematika yang mempelajari hubungan antara sudut dan sisi-sisi segitiga. Dalam trigonometri, kita menggunakan fungsi-fungsi trigonometri seperti sinus (sin), kosinus (cos), dan tangen (tan) untuk menghitung sisi-sisi segitiga berdasarkan sudut yang diketahui, atau sebaliknya.

Trigonometri memiliki aplikasi yang luas dalam berbagai bidang, termasuk navigasi, survei, fisika, dan teknik. Pemahaman tentang sudut dan fungsi trigonometri sangat penting untuk memecahkan masalah-masalah yang melibatkan segitiga dan gelombang.

Sudut dalam Geometri Lanjut: Lebih dari Sekadar Garis

Dalam geometri lanjut, konsep sudut diperluas untuk mencakup sudut antara bidang, sudut antara garis dan bidang, dan sudut dalam ruang tiga dimensi. Pemahaman tentang sudut dalam ruang tiga dimensi sangat penting dalam bidang-bidang seperti grafika komputer, desain 3D, dan arsitektur.

Selain itu, dalam geometri non-Euclidean, konsep sudut dapat berbeda dari yang kita kenal dalam geometri Euclidean. Misalnya, dalam geometri bola, jumlah sudut dalam segitiga bisa lebih besar dari 180°.

Kesimpulan: Sudut sebagai Pilar Geometri

Sudut adalah konsep fundamental dalam geometri yang memiliki aplikasi luas dalam berbagai bidang kehidupan. Pemahaman mendalam tentang jenis-jenis sudut, hubungan antar sudut, dan cara mengukurnya sangat penting untuk memecahkan masalah-masalah geometri yang kompleks dan menerapkan konsep geometri dalam kehidupan sehari-hari.

Dengan memahami sudut, kita dapat memahami dunia di sekitar kita dengan lebih baik, mulai dari arsitektur bangunan hingga gerakan benda-benda langit. Sudut adalah pilar penting dalam geometri yang membuka pintu menuju pemahaman yang lebih dalam tentang bentuk dan ruang.

Semoga artikel ini bermanfaat bagi Anda dalam memahami konsep sudut dan aplikasinya. Teruslah belajar dan eksplorasi dunia geometri yang menarik!

Tabel Jenis-Jenis Sudut:

Jenis Sudut Ukuran Contoh

Sudut Lancip	> 0° dan < 90°	Ujung pensil
Sudut Siku-Siku	90°	Sudut ruangan
Sudut Tumpul	> 90° dan < 180°	Posisi jarum jam pukul 2
Sudut Lurus	180°	Garis lurus
Sudut Refleks	> 180° dan < 360°	Putaran hampir lengkap
Sudut Penuh	360°	Lingkaran penuh

Rumus Penting Terkait Sudut:

• Sudut Berpenyiku: ∠A + ∠B = 90°
• Sudut Berpelurus: ∠A + ∠B = 180°

Soal Latihan:

1. Tentukan jenis sudut yang terbentuk jika jarum jam menunjukkan pukul 3.
2. Jika ∠A = 45°, tentukan ukuran sudut penyikunya.
3. Jika ∠B = 135°, tentukan ukuran sudut pelurusnya.

Jawaban:

1. Sudut siku-siku
2. 45°
3. 45°

Referensi Tambahan:

• Buku teks matematika sekolah menengah
• Situs web matematika online
• Video pembelajaran tentang sudut

Pentingnya Ketelitian dalam Pengukuran Sudut:

Dalam banyak aplikasi praktis, ketelitian dalam pengukuran sudut sangat penting. Kesalahan kecil dalam pengukuran sudut dapat menyebabkan kesalahan yang signifikan dalam hasil akhir. Oleh karena itu, penting untuk menggunakan alat ukur yang tepat dan mengikuti prosedur pengukuran yang benar.

Peran Teknologi dalam Pengukuran Sudut:

Perkembangan teknologi telah membawa kemajuan yang signifikan dalam pengukuran sudut. Alat-alat ukur modern seperti teodolit digital dan total station memungkinkan pengukuran sudut dengan akurasi yang sangat tinggi. Selain itu, perangkat lunak komputer dapat digunakan untuk memproses data pengukuran sudut dan menghasilkan model 3D yang akurat.

Sudut dalam Seni dan Budaya:

Sudut juga memiliki peran penting dalam seni dan budaya. Dalam seni rupa, sudut digunakan untuk menciptakan perspektif dan ilusi kedalaman. Dalam arsitektur, sudut digunakan untuk menciptakan desain yang estetis dan fungsional. Dalam budaya, sudut dapat memiliki makna simbolis yang berbeda-beda.

Sudut dan Simetri:

Sudut memiliki hubungan yang erat dengan simetri. Benda-benda yang simetris memiliki sudut-sudut yang sama atau berhubungan. Simetri dapat ditemukan dalam berbagai bentuk alam dan buatan manusia, mulai dari kristal hingga bangunan.

Sudut dalam Alam:

Sudut dapat ditemukan di mana-mana di alam. Sudut antara cabang pohon, sudut antara kelopak bunga, dan sudut antara sisi-sisi kristal adalah beberapa contoh sudut yang dapat ditemukan di alam. Mempelajari sudut dalam alam dapat membantu kita memahami prinsip-prinsip desain dan struktur yang mendasarinya.

Sudut dan Musik:

Meskipun tidak terlihat secara langsung, sudut juga memiliki hubungan dengan musik. Interval musik, seperti oktaf, kuint, dan kuart, dapat direpresentasikan sebagai sudut pada lingkaran. Hubungan antara sudut dan musik telah dipelajari oleh para matematikawan dan musisi selama berabad-abad.

Sudut dan Astronomi:

Dalam astronomi, sudut digunakan untuk mengukur posisi dan jarak benda-benda langit. Sudut elevasi, sudut azimut, dan sudut paralaks adalah beberapa contoh sudut yang penting dalam astronomi. Pengukuran sudut yang akurat sangat penting untuk memahami alam semesta.

Sudut dan Robotika:

Dalam robotika, sudut digunakan untuk mengontrol gerakan robot. Sudut sendi, sudut rotasi, dan sudut kemiringan adalah beberapa contoh sudut yang penting dalam robotika. Pemahaman tentang sudut sangat penting untuk merancang dan memprogram robot yang dapat bergerak dengan presisi.

Sudut dan Permainan:

Sudut juga memiliki peran dalam permainan, baik permainan tradisional maupun permainan video. Sudut lemparan, sudut pantulan, dan sudut pandang adalah beberapa contoh sudut yang penting dalam permainan. Memahami sudut dapat membantu pemain meningkatkan keterampilan mereka.

Sudut dan Pendidikan:

Pemahaman tentang sudut merupakan bagian penting dari pendidikan matematika. Mempelajari sudut membantu siswa mengembangkan kemampuan berpikir logis, kemampuan memecahkan masalah, dan kemampuan visualisasi. Konsep sudut diajarkan sejak sekolah dasar dan terus dikembangkan di tingkat pendidikan yang lebih tinggi.

Sudut dan Masa Depan:

Konsep sudut akan terus relevan di masa depan. Dengan perkembangan teknologi yang pesat, pemahaman tentang sudut akan semakin penting dalam berbagai bidang, seperti robotika, kecerdasan buatan, dan realitas virtual. Teruslah belajar dan eksplorasi dunia sudut yang tak terbatas!