Rumus Deret Geometri: Memahami Deret Angka

Ilustrasi(Youtube FKIP Unej Official)

Dalam dunia matematika, deret geometri memegang peranan penting sebagai salah satu konsep fundamental yang sering diaplikasikan dalam berbagai bidang. Deret ini, dengan karakteristik uniknya, menawarkan pola yang teratur dan dapat diprediksi, memungkinkan kita untuk menganalisis dan memahami fenomena yang melibatkan pertumbuhan atau penyusutan eksponensial. Memahami rumus deret geometri bukan hanya sekadar menghafal formula, tetapi juga tentang menguasai logika di balik pembentukan deret tersebut dan bagaimana ia dapat digunakan untuk memecahkan masalah.

Mengenal Lebih Dekat Deret Geometri

Deret geometri adalah urutan angka di mana setiap suku diperoleh dengan mengalikan suku sebelumnya dengan suatu bilangan tetap yang disebut rasio. Rasio ini menjadi kunci utama dalam mengidentifikasi dan menganalisis deret geometri. Jika rasio bernilai positif, deret akan menunjukkan pertumbuhan eksponensial, sedangkan rasio negatif akan menghasilkan deret yang berosilasi antara nilai positif dan negatif. Pemahaman mendalam tentang rasio ini sangat penting untuk memprediksi perilaku deret dan menghitung jumlah suku-sukunya.

Perbedaan mendasar antara deret geometri dan deret aritmatika terletak pada cara pembentukan suku-sukunya. Dalam deret aritmatika, setiap suku diperoleh dengan menambahkan selisih tetap ke suku sebelumnya. Sementara itu, dalam deret geometri, setiap suku diperoleh dengan mengalikan suku sebelumnya dengan rasio tetap. Perbedaan ini menghasilkan karakteristik yang berbeda pula pada kedua jenis deret tersebut. Deret aritmatika cenderung menunjukkan pertumbuhan atau penurunan linear, sedangkan deret geometri menunjukkan pertumbuhan atau penurunan eksponensial.

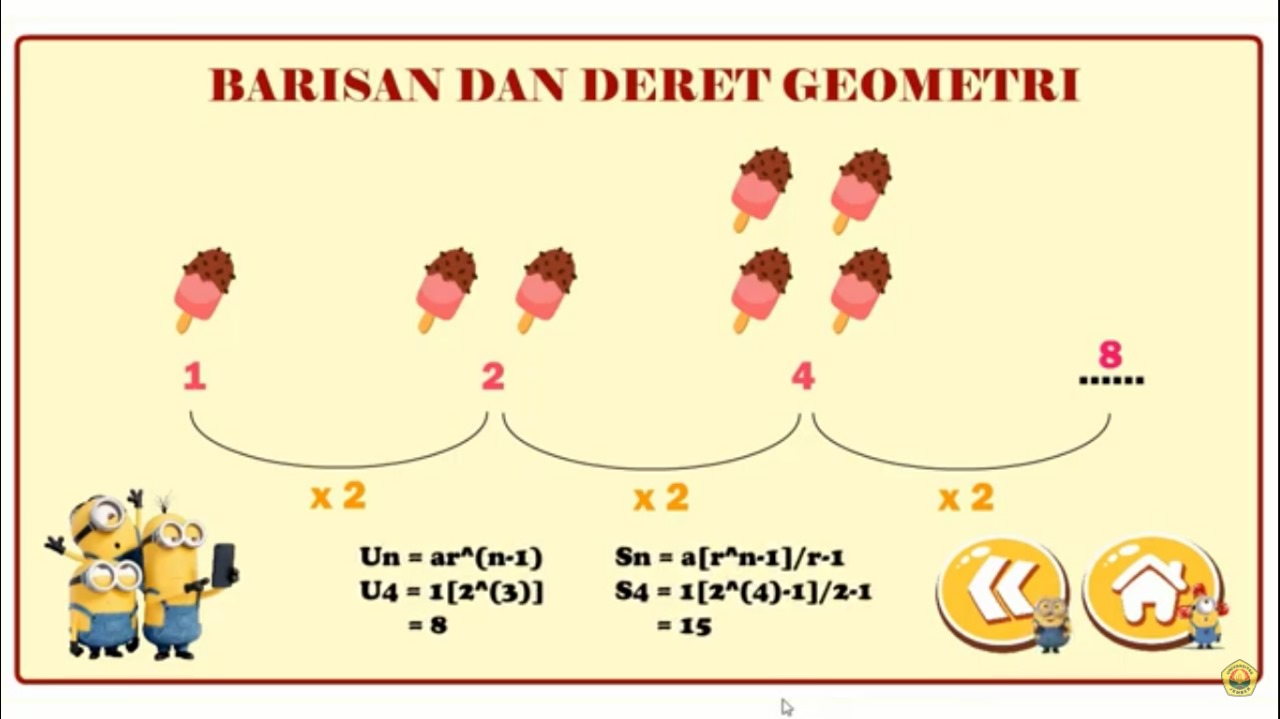
Contoh sederhana deret geometri adalah 2, 4, 8, 16, 32, dan seterusnya. Dalam deret ini, rasio adalah 2, karena setiap suku diperoleh dengan mengalikan suku sebelumnya dengan 2. Contoh lain adalah 1, -3, 9, -27, 81, dan seterusnya. Dalam deret ini, rasio adalah -3, yang menghasilkan deret dengan suku-suku yang bergantian antara positif dan negatif.

Penerapan deret geometri sangat luas dan dapat ditemukan dalam berbagai bidang, seperti keuangan, fisika, dan ilmu komputer. Dalam keuangan, deret geometri digunakan untuk menghitung nilai investasi dengan bunga majemuk. Dalam fisika, deret geometri digunakan untuk memodelkan peluruhan radioaktif. Dalam ilmu komputer, deret geometri digunakan dalam analisis algoritma dan struktur data.

Rumus Dasar Deret Geometri

Rumus dasar deret geometri terdiri dari dua jenis, yaitu rumus untuk mencari suku ke-n dan rumus untuk mencari jumlah n suku pertama. Kedua rumus ini sangat penting untuk memahami dan menganalisis deret geometri secara komprehensif.

Rumus Suku ke-n:

Suku ke-n (Un) dari deret geometri dapat dihitung menggunakan rumus:

Un = a r^(n-1)

di mana:

• a adalah suku pertama
• r adalah rasio
• n adalah nomor suku yang ingin dicari

Rumus ini memungkinkan kita untuk mencari suku ke-n tanpa harus menghitung semua suku sebelumnya. Misalnya, jika kita ingin mencari suku ke-10 dari deret geometri dengan suku pertama 2 dan rasio 3, kita dapat langsung menggunakan rumus tersebut untuk mendapatkan hasilnya.

Rumus Jumlah n Suku Pertama:

Jumlah n suku pertama (Sn) dari deret geometri dapat dihitung menggunakan rumus:

Sn = a (1 - r^n) / (1 - r) (untuk r ≠ 1)

atau

Sn = n a (untuk r = 1)

di mana:

• a adalah suku pertama
• r adalah rasio
• n adalah jumlah suku yang ingin dijumlahkan

Rumus ini memungkinkan kita untuk menghitung jumlah n suku pertama dengan cepat dan efisien. Misalnya, jika kita ingin menghitung jumlah 5 suku pertama dari deret geometri dengan suku pertama 1 dan rasio 2, kita dapat langsung menggunakan rumus tersebut untuk mendapatkan hasilnya.

Penting untuk diingat bahwa rumus jumlah n suku pertama hanya berlaku jika rasio tidak sama dengan 1. Jika rasio sama dengan 1, maka deret tersebut menjadi deret aritmatika dengan selisih 0, dan jumlah n suku pertamanya dapat dihitung dengan mengalikan suku pertama dengan jumlah suku.

Contoh Soal dan Pembahasan

Untuk memperdalam pemahaman tentang rumus deret geometri, mari kita bahas beberapa contoh soal beserta pembahasannya:

Contoh Soal 1:

Tentukan suku ke-7 dari deret geometri 3, 6, 12, 24, ...

Pembahasan:

Suku pertama (a) = 3

Rasio (r) = 6 / 3 = 2

n = 7

Un = a r^(n-1)

U7 = 3 2^(7-1)

U7 = 3 2^6

U7 = 3 64

U7 = 192

Jadi, suku ke-7 dari deret geometri tersebut adalah 192.

Contoh Soal 2:

Hitunglah jumlah 6 suku pertama dari deret geometri 2, 6, 18, 54, ...

Pembahasan:

Suku pertama (a) = 2

Rasio (r) = 6 / 2 = 3

n = 6

Sn = a (1 - r^n) / (1 - r)

S6 = 2 (1 - 3^6) / (1 - 3)

S6 = 2 (1 - 729) / (-2)

S6 = 2 (-728) / (-2)

S6 = 728

Jadi, jumlah 6 suku pertama dari deret geometri tersebut adalah 728.

Contoh Soal 3:

Sebuah bola dijatuhkan dari ketinggian 10 meter. Setiap kali memantul, bola mencapai ketinggian 3/4 dari ketinggian sebelumnya. Hitunglah panjang lintasan bola sampai berhenti.

Pembahasan:

Soal ini melibatkan deret geometri tak hingga. Panjang lintasan bola terdiri dari lintasan turun dan lintasan naik.

Lintasan turun: 10 + 10(3/4) + 10(3/4)^2 + ...

Lintasan naik: 10(3/4) + 10(3/4)^2 + 10(3/4)^3 + ...

Suku pertama (a) untuk lintasan turun = 10

Suku pertama (a) untuk lintasan naik = 10(3/4) = 7.5

Rasio (r) = 3/4

Jumlah deret geometri tak hingga (S∞) = a / (1 - r)

Jumlah lintasan turun = 10 / (1 - 3/4) = 10 / (1/4) = 40

Jumlah lintasan naik = 7.5 / (1 - 3/4) = 7.5 / (1/4) = 30

Panjang lintasan total = Jumlah lintasan turun + Jumlah lintasan naik = 40 + 30 = 70

Jadi, panjang lintasan bola sampai berhenti adalah 70 meter.

Deret Geometri Tak Hingga

Deret geometri tak hingga adalah deret geometri dengan jumlah suku yang tidak terbatas. Deret ini memiliki karakteristik yang unik, terutama dalam hal konvergensi dan divergensi. Konvergensi terjadi ketika jumlah suku-suku deret mendekati suatu nilai tertentu, sedangkan divergensi terjadi ketika jumlah suku-suku deret terus bertambah tanpa batas.

Konvergensi dan Divergensi:

Deret geometri tak hingga konvergen jika nilai mutlak rasio (|r|) kurang dari 1 (|r| < 1). Dalam kondisi ini, jumlah deret dapat dihitung menggunakan rumus:

S∞ = a / (1 - r)

di mana:

• a adalah suku pertama
• r adalah rasio

Jika nilai mutlak rasio lebih besar atau sama dengan 1 (|r| ≥ 1), maka deret geometri tak hingga divergen, dan jumlahnya tidak dapat dihitung.

Aplikasi Deret Geometri Tak Hingga:

Deret geometri tak hingga memiliki banyak aplikasi dalam berbagai bidang, seperti:

• Representasi Desimal Berulang: Bilangan desimal berulang dapat direpresentasikan sebagai deret geometri tak hingga. Misalnya, 0.333... dapat direpresentasikan sebagai 3/10 + 3/100 + 3/1000 + ..., yang merupakan deret geometri dengan suku pertama 3/10 dan rasio 1/10.
• Fisika: Dalam fisika, deret geometri tak hingga digunakan untuk memodelkan berbagai fenomena, seperti peluruhan radioaktif dan osilasi teredam.
• Ekonomi: Dalam ekonomi, deret geometri tak hingga digunakan untuk menghitung nilai sekarang dari anuitas dan investasi dengan pertumbuhan konstan.

Tips dan Trik dalam Menyelesaikan Soal Deret Geometri

Berikut adalah beberapa tips dan trik yang dapat membantu Anda dalam menyelesaikan soal deret geometri:

• Identifikasi Suku Pertama dan Rasio: Langkah pertama dalam menyelesaikan soal deret geometri adalah mengidentifikasi suku pertama (a) dan rasio (r). Rasio dapat dihitung dengan membagi suku kedua dengan suku pertama, atau suku ketiga dengan suku kedua, dan seterusnya.
• Perhatikan Tanda Rasio: Tanda rasio (positif atau negatif) sangat penting karena mempengaruhi perilaku deret. Rasio positif akan menghasilkan deret dengan suku-suku yang memiliki tanda yang sama, sedangkan rasio negatif akan menghasilkan deret dengan suku-suku yang bergantian tanda.
• Gunakan Rumus yang Tepat: Pastikan Anda menggunakan rumus yang tepat sesuai dengan jenis soal yang diberikan. Jika soal meminta untuk mencari suku ke-n, gunakan rumus suku ke-n. Jika soal meminta untuk mencari jumlah n suku pertama, gunakan rumus jumlah n suku pertama. Jika soal melibatkan deret geometri tak hingga, gunakan rumus jumlah deret geometri tak hingga (jika konvergen).
• Sederhanakan Persamaan: Setelah memasukkan nilai-nilai yang diketahui ke dalam rumus, sederhanakan persamaan tersebut untuk mendapatkan jawaban yang benar.
• Periksa Kembali Jawaban: Setelah mendapatkan jawaban, periksa kembali jawaban tersebut untuk memastikan bahwa jawaban tersebut masuk akal dan sesuai dengan konteks soal.
• Latihan Soal: Semakin banyak Anda berlatih soal deret geometri, semakin mahir Anda dalam menyelesaikan soal-soal tersebut. Carilah berbagai jenis soal deret geometri dari berbagai sumber dan cobalah untuk menyelesaikannya.

Penerapan Deret Geometri dalam Kehidupan Sehari-hari

Meskipun terlihat abstrak, deret geometri sebenarnya memiliki banyak penerapan dalam kehidupan sehari-hari. Berikut adalah beberapa contohnya:

• Perhitungan Bunga Majemuk: Bunga majemuk adalah bunga yang dihitung berdasarkan pokok pinjaman awal dan juga akumulasi bunga dari periode sebelumnya. Perhitungan bunga majemuk melibatkan deret geometri, di mana setiap periode bunga ditambahkan ke pokok pinjaman, sehingga pokok pinjaman terus bertambah secara eksponensial.
• Perencanaan Keuangan: Deret geometri dapat digunakan untuk merencanakan keuangan, seperti menghitung nilai investasi di masa depan atau menentukan jumlah tabungan yang dibutuhkan untuk mencapai tujuan keuangan tertentu.
• Pertumbuhan Populasi: Pertumbuhan populasi seringkali dimodelkan menggunakan deret geometri, di mana populasi meningkat secara eksponensial setiap tahunnya.
• Penyebaran Virus: Penyebaran virus juga dapat dimodelkan menggunakan deret geometri, di mana jumlah orang yang terinfeksi virus meningkat secara eksponensial setiap harinya.
• Desain Arsitektur: Beberapa desain arsitektur menggunakan prinsip deret geometri untuk menciptakan struktur yang estetis dan proporsional.
• Musik: Dalam musik, deret geometri dapat digunakan untuk mengatur interval nada dan menciptakan harmoni yang indah.

Kesimpulan

Rumus deret geometri adalah alat yang ampuh untuk memahami dan menganalisis pola pertumbuhan atau penyusutan eksponensial. Dengan memahami rumus dasar, contoh soal, dan tips-tips yang telah dibahas, Anda dapat menguasai konsep deret geometri dan mengaplikasikannya dalam berbagai bidang. Jangan ragu untuk terus berlatih dan mengeksplorasi berbagai jenis soal deret geometri untuk memperdalam pemahaman Anda.

Pemahaman yang mendalam tentang deret geometri tidak hanya bermanfaat dalam matematika, tetapi juga dalam berbagai aspek kehidupan lainnya. Dengan menguasai konsep ini, Anda akan memiliki kemampuan untuk menganalisis dan memecahkan masalah yang melibatkan pertumbuhan atau penyusutan eksponensial dengan lebih efektif.

Jadi, teruslah belajar dan eksplorasi dunia matematika yang menarik ini! Siapa tahu, Anda akan menemukan aplikasi deret geometri yang baru dan inovatif yang dapat memberikan kontribusi positif bagi masyarakat.