Bangun Ruang: Memahami Geometri Tiga Dimensi

Ilustrasi(Pinterest)

Dalam dunia matematika, selain berurusan dengan objek dua dimensi seperti garis dan bidang datar, kita juga menjelajahi objek yang memiliki volume dan kedalaman, yang dikenal sebagai bangun ruang. Pemahaman tentang bangun ruang sangat penting dalam berbagai bidang, mulai dari arsitektur dan teknik sipil hingga desain grafis dan pengembangan game. Artikel ini akan membahas berbagai jenis bangun ruang, sifat-sifatnya, rumus-rumus penting, serta aplikasinya dalam kehidupan sehari-hari.

Jenis-Jenis Bangun Ruang dan Karakteristiknya

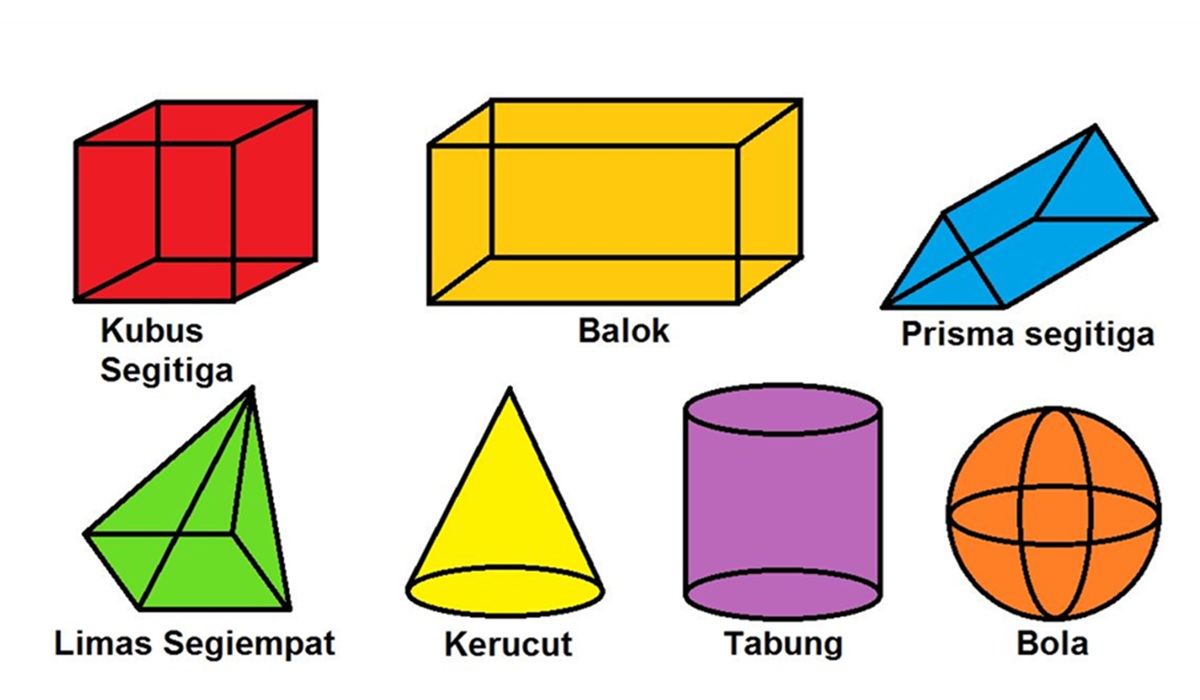
Bangun ruang dapat diklasifikasikan menjadi beberapa kategori utama, masing-masing dengan karakteristik uniknya. Berikut adalah beberapa jenis bangun ruang yang paling umum:

Kubus: Kubus adalah bangun ruang yang paling sederhana, terdiri dari enam sisi yang semuanya berbentuk persegi identik. Semua sudut kubus adalah sudut siku-siku, dan semua rusuknya memiliki panjang yang sama. Kubus memiliki 8 titik sudut dan 12 rusuk.

Balok: Balok mirip dengan kubus, tetapi sisi-sisinya tidak harus semuanya berbentuk persegi. Balok memiliki enam sisi yang berbentuk persegi panjang, dengan sisi-sisi yang berhadapan memiliki ukuran yang sama. Seperti kubus, balok juga memiliki 8 titik sudut dan 12 rusuk.

Prisma: Prisma adalah bangun ruang yang memiliki dua sisi yang kongruen dan sejajar, yang disebut alas dan tutup. Sisi-sisi lainnya berbentuk persegi panjang atau jajar genjang. Prisma dinamai berdasarkan bentuk alasnya, misalnya prisma segitiga, prisma segiempat, prisma pentagonal, dan seterusnya. Tinggi prisma adalah jarak tegak lurus antara alas dan tutup.

Limas: Limas adalah bangun ruang yang memiliki alas berbentuk poligon dan sisi-sisi tegak yang berbentuk segitiga yang bertemu di satu titik, yang disebut puncak limas. Seperti prisma, limas juga dinamai berdasarkan bentuk alasnya, misalnya limas segitiga, limas segiempat, limas pentagonal, dan seterusnya. Tinggi limas adalah jarak tegak lurus dari puncak ke alas.

Tabung: Tabung adalah bangun ruang yang memiliki dua alas berbentuk lingkaran yang kongruen dan sejajar, serta sebuah selimut yang berbentuk persegi panjang yang melengkung. Jari-jari tabung adalah jari-jari lingkaran alas, dan tinggi tabung adalah jarak antara kedua alas.

Kerucut: Kerucut adalah bangun ruang yang memiliki alas berbentuk lingkaran dan sebuah sisi tegak yang melengkung dan bertemu di satu titik, yang disebut puncak kerucut. Jari-jari kerucut adalah jari-jari lingkaran alas, dan tinggi kerucut adalah jarak tegak lurus dari puncak ke alas.

Bola: Bola adalah bangun ruang yang terdiri dari semua titik yang berjarak sama dari satu titik pusat. Jarak ini disebut jari-jari bola. Bola tidak memiliki sisi atau rusuk.

Rumus-Rumus Penting dalam Bangun Ruang

Untuk menghitung volume dan luas permukaan bangun ruang, kita menggunakan rumus-rumus tertentu yang didasarkan pada dimensi dan bentuk bangun ruang tersebut. Berikut adalah beberapa rumus penting yang perlu diketahui:

Kubus:

• Volume (V) = s³, di mana s adalah panjang sisi kubus.
• Luas Permukaan (L) = 6s²

Balok:

• Volume (V) = p x l x t, di mana p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
• Luas Permukaan (L) = 2(pl + pt + lt)

Prisma:

• Volume (V) = Luas Alas x Tinggi
• Luas Permukaan (L) = 2 x Luas Alas + Luas Selimut

Limas:

• Volume (V) = (1/3) x Luas Alas x Tinggi
• Luas Permukaan (L) = Luas Alas + Luas Sisi Tegak

Tabung:

• Volume (V) = πr²t, di mana r adalah jari-jari alas dan t adalah tinggi tabung.
• Luas Permukaan (L) = 2πr² + 2πrt

Kerucut:

• Volume (V) = (1/3)πr²t, di mana r adalah jari-jari alas dan t adalah tinggi kerucut.
• Luas Permukaan (L) = πr² + πrs, di mana s adalah garis pelukis kerucut (s = √(r² + t²)).

Bola:

• Volume (V) = (4/3)πr³, di mana r adalah jari-jari bola.
• Luas Permukaan (L) = 4πr²

Aplikasi Bangun Ruang dalam Kehidupan Sehari-hari

Konsep bangun ruang tidak hanya relevan dalam matematika, tetapi juga memiliki aplikasi yang luas dalam kehidupan sehari-hari. Berikut adalah beberapa contohnya:

Arsitektur dan Teknik Sipil: Bangun ruang digunakan untuk merancang dan membangun bangunan, jembatan, dan infrastruktur lainnya. Pemahaman tentang volume, luas permukaan, dan kekuatan material sangat penting untuk memastikan keamanan dan stabilitas struktur.

Desain Grafis dan Pengembangan Game: Bangun ruang digunakan untuk membuat model 3D dan animasi dalam desain grafis dan pengembangan game. Objek-objek dalam game dan animasi sering kali direpresentasikan sebagai bangun ruang dengan tekstur dan pencahayaan yang realistis.

Kemasan Produk: Bentuk dan ukuran kemasan produk sering kali didasarkan pada konsep bangun ruang. Tujuannya adalah untuk memaksimalkan ruang penyimpanan, melindungi produk dari kerusakan, dan menarik perhatian konsumen.

Pembuatan Furnitur: Desain furnitur seperti meja, kursi, dan lemari melibatkan pemahaman tentang bangun ruang. Dimensi dan bentuk furnitur harus sesuai dengan ruang yang tersedia dan memenuhi kebutuhan pengguna.

Astronomi: Bentuk planet, bintang, dan benda langit lainnya dapat diaproksimasi sebagai bangun ruang, seperti bola atau elipsoid. Pemahaman tentang volume dan luas permukaan benda langit penting untuk menghitung massa, gravitasi, dan karakteristik lainnya.

Memahami Lebih Dalam tentang Kubus dan Balok

Kubus dan balok adalah dua bangun ruang yang paling sering kita temui dalam kehidupan sehari-hari. Mari kita telaah lebih dalam tentang sifat-sifat dan karakteristiknya.

Kubus: Kubus adalah bentuk yang sangat simetris. Setiap sisi, rusuk, dan sudutnya identik. Simetri ini membuat kubus menjadi bentuk yang stabil dan mudah diprediksi. Dalam matematika, kubus sering digunakan sebagai contoh dasar untuk memahami konsep volume dan luas permukaan. Dalam kehidupan nyata, kita dapat menemukan kubus dalam bentuk dadu, kotak kardus, atau bahkan bangunan modern dengan desain minimalis.

Balok: Balok, meskipun mirip dengan kubus, memiliki fleksibilitas yang lebih besar dalam hal dimensi. Panjang, lebar, dan tinggi balok dapat berbeda-beda, memungkinkan kita untuk menciptakan berbagai macam bentuk dan ukuran. Balok sering digunakan dalam konstruksi bangunan, pembuatan furnitur, dan desain kemasan. Kemampuan balok untuk menyesuaikan diri dengan berbagai kebutuhan menjadikannya bentuk yang sangat serbaguna.

Perbedaan utama antara kubus dan balok terletak pada kesamaan sisi-sisinya. Kubus memiliki semua sisi yang sama (persegi), sedangkan balok memiliki sisi-sisi yang berbentuk persegi panjang yang tidak harus sama. Namun, keduanya memiliki kesamaan dalam hal jumlah sisi, rusuk, dan titik sudut.

Menjelajahi Prisma dan Limas: Bangun Ruang dengan Variasi Bentuk

Prisma dan limas menawarkan variasi bentuk yang lebih luas dibandingkan kubus dan balok. Bentuk alas prisma dan limas dapat berupa segitiga, segiempat, pentagon, atau poligon lainnya, sehingga menciptakan berbagai macam bangun ruang yang unik.

Prisma: Prisma memiliki dua alas yang identik dan sejajar, serta sisi-sisi tegak yang menghubungkan kedua alas tersebut. Bentuk alas prisma menentukan nama prisma tersebut. Misalnya, prisma segitiga memiliki alas berbentuk segitiga, prisma segiempat memiliki alas berbentuk segiempat, dan seterusnya. Volume prisma dihitung dengan mengalikan luas alas dengan tinggi prisma. Prisma sering digunakan dalam desain arsitektur, optik (seperti prisma yang memecah cahaya menjadi warna-warna pelangi), dan dalam pembuatan lensa.

Limas: Limas memiliki alas berbentuk poligon dan sisi-sisi tegak yang berbentuk segitiga yang bertemu di satu titik, yang disebut puncak limas. Seperti prisma, nama limas ditentukan oleh bentuk alasnya. Misalnya, limas segitiga memiliki alas berbentuk segitiga, limas segiempat memiliki alas berbentuk segiempat, dan seterusnya. Volume limas dihitung dengan rumus (1/3) x Luas Alas x Tinggi. Limas sering dikaitkan dengan piramida Mesir kuno, yang merupakan contoh arsitektur megah yang menggunakan bentuk limas.

Perbedaan utama antara prisma dan limas adalah jumlah alasnya dan bentuk sisi-sisi tegaknya. Prisma memiliki dua alas yang identik, sedangkan limas hanya memiliki satu alas. Sisi-sisi tegak prisma berbentuk persegi panjang atau jajar genjang, sedangkan sisi-sisi tegak limas berbentuk segitiga.

Memahami Tabung, Kerucut, dan Bola: Bangun Ruang dengan Bentuk Melengkung

Tabung, kerucut, dan bola adalah bangun ruang yang memiliki permukaan melengkung. Bentuk melengkung ini memberikan karakteristik unik dan aplikasi yang berbeda dibandingkan dengan bangun ruang yang memiliki sisi-sisi datar.

Tabung: Tabung memiliki dua alas berbentuk lingkaran yang identik dan sejajar, serta sebuah selimut yang menghubungkan kedua alas tersebut. Volume tabung dihitung dengan rumus πr²t, di mana r adalah jari-jari alas dan t adalah tinggi tabung. Tabung sering digunakan dalam pembuatan pipa, kaleng minuman, dan wadah silinder lainnya. Kekuatan dan efisiensi tabung dalam menahan tekanan menjadikannya bentuk yang ideal untuk berbagai aplikasi industri.

Kerucut: Kerucut memiliki alas berbentuk lingkaran dan sebuah sisi tegak yang melengkung dan bertemu di satu titik, yang disebut puncak kerucut. Volume kerucut dihitung dengan rumus (1/3)πr²t, di mana r adalah jari-jari alas dan t adalah tinggi kerucut. Kerucut sering digunakan dalam pembuatan topi ulang tahun, corong, dan bagian-bagian mesin. Bentuk kerucut yang meruncing memungkinkan aliran fluida atau material dengan mudah.

Bola: Bola adalah bangun ruang yang terdiri dari semua titik yang berjarak sama dari satu titik pusat. Jarak ini disebut jari-jari bola. Volume bola dihitung dengan rumus (4/3)πr³, dan luas permukaannya dihitung dengan rumus 4πr². Bola adalah bentuk yang sangat efisien dalam hal volume dan luas permukaan. Bola sering digunakan dalam pembuatan bola olahraga, bantalan, dan dalam representasi planet dan bintang dalam astronomi.

Perbedaan utama antara tabung, kerucut, dan bola terletak pada bentuk alas dan sisi-sisi tegaknya. Tabung memiliki dua alas berbentuk lingkaran, kerucut memiliki satu alas berbentuk lingkaran, dan bola tidak memiliki alas. Tabung memiliki selimut yang berbentuk persegi panjang yang melengkung, kerucut memiliki sisi tegak yang melengkung dan bertemu di satu titik, dan bola memiliki permukaan yang melengkung secara merata.

Penerapan Konsep Bangun Ruang dalam Teknologi Modern

Konsep bangun ruang tidak hanya penting dalam matematika dan ilmu pengetahuan, tetapi juga memainkan peran penting dalam teknologi modern. Berikut adalah beberapa contoh penerapan konsep bangun ruang dalam teknologi:

Pemodelan 3D: Dalam desain grafis, animasi, dan pengembangan game, pemodelan 3D digunakan untuk menciptakan objek dan lingkungan virtual yang realistis. Objek-objek ini direpresentasikan sebagai bangun ruang dengan tekstur, pencahayaan, dan efek visual lainnya. Pemodelan 3D memungkinkan kita untuk memvisualisasikan dan berinteraksi dengan objek dalam ruang tiga dimensi sebelum objek tersebut dibuat secara fisik.

Pencetakan 3D: Pencetakan 3D adalah teknologi yang memungkinkan kita untuk membuat objek tiga dimensi dari desain digital. Proses ini melibatkan pembuatan lapisan-lapisan material secara berturut-turut hingga objek selesai terbentuk. Konsep bangun ruang sangat penting dalam pencetakan 3D, karena desain objek harus dipecah menjadi lapisan-lapisan yang dapat dicetak.

Realitas Virtual (VR) dan Realitas Tertambah (AR): VR dan AR adalah teknologi yang menciptakan pengalaman imersif dengan menggabungkan dunia nyata dan dunia virtual. Dalam VR, pengguna sepenuhnya tenggelam dalam lingkungan virtual, sedangkan dalam AR, objek virtual ditambahkan ke dunia nyata. Konsep bangun ruang digunakan untuk menciptakan objek dan lingkungan virtual yang realistis dalam VR dan AR.

Robotika: Robot sering kali dirancang untuk berinteraksi dengan lingkungan fisik. Pemahaman tentang bangun ruang sangat penting dalam robotika, karena robot harus dapat mengenali, memanipulasi, dan bergerak di sekitar objek tiga dimensi. Robot menggunakan sensor dan algoritma untuk memahami geometri lingkungan mereka dan merencanakan gerakan yang sesuai.

Pemindaian 3D: Pemindaian 3D adalah teknologi yang memungkinkan kita untuk membuat model digital dari objek fisik. Proses ini melibatkan penggunaan sensor untuk mengukur dimensi dan bentuk objek, dan kemudian merekonstruksi model 3D dari data tersebut. Pemindaian 3D digunakan dalam berbagai aplikasi, seperti arkeologi, manufaktur, dan kedokteran.

Tips dan Trik dalam Mempelajari Bangun Ruang

Mempelajari bangun ruang bisa menjadi tantangan, tetapi dengan pendekatan yang tepat, Anda dapat menguasai konsep-konsep ini dengan lebih mudah. Berikut adalah beberapa tips dan trik yang dapat membantu Anda:

Visualisasikan Bangun Ruang: Cobalah untuk membayangkan bangun ruang dalam pikiran Anda. Gunakan objek-objek di sekitar Anda sebagai contoh untuk membantu Anda memvisualisasikan bentuk dan dimensi bangun ruang.

Gunakan Model Fisik: Membuat atau menggunakan model fisik bangun ruang dapat membantu Anda memahami sifat-sifat dan karakteristiknya dengan lebih baik. Anda dapat menggunakan kertas, karton, atau bahan lainnya untuk membuat model sederhana.

Kerjakan Soal-Soal Latihan: Mengerjakan soal-soal latihan adalah cara terbaik untuk menguji pemahaman Anda tentang konsep bangun ruang. Mulailah dengan soal-soal yang mudah dan secara bertahap tingkatkan kesulitan soal.

Gunakan Sumber Daya Online: Ada banyak sumber daya online yang tersedia untuk membantu Anda mempelajari bangun ruang, seperti video tutorial, simulasi interaktif, dan latihan soal.

Berkolaborasi dengan Teman: Belajar bersama teman dapat membantu Anda memahami konsep-konsep yang sulit dan memecahkan soal-soal yang menantang. Diskusikan konsep-konsep yang Anda pelajari dan saling membantu dalam mengerjakan soal-soal latihan.

Jangan Takut Bertanya: Jika Anda mengalami kesulitan dalam memahami konsep bangun ruang, jangan takut untuk bertanya kepada guru, teman, atau ahli matematika.

Kesimpulan

Bangun ruang adalah bagian penting dari geometri dan memiliki aplikasi yang luas dalam berbagai bidang. Dengan memahami jenis-jenis bangun ruang, sifat-sifatnya, rumus-rumus penting, dan aplikasinya, Anda dapat mengembangkan pemahaman yang lebih mendalam tentang dunia di sekitar Anda. Teruslah berlatih dan menjelajahi konsep-konsep bangun ruang, dan Anda akan menemukan bahwa matematika bisa menjadi subjek yang menarik dan bermanfaat. (Z-2)