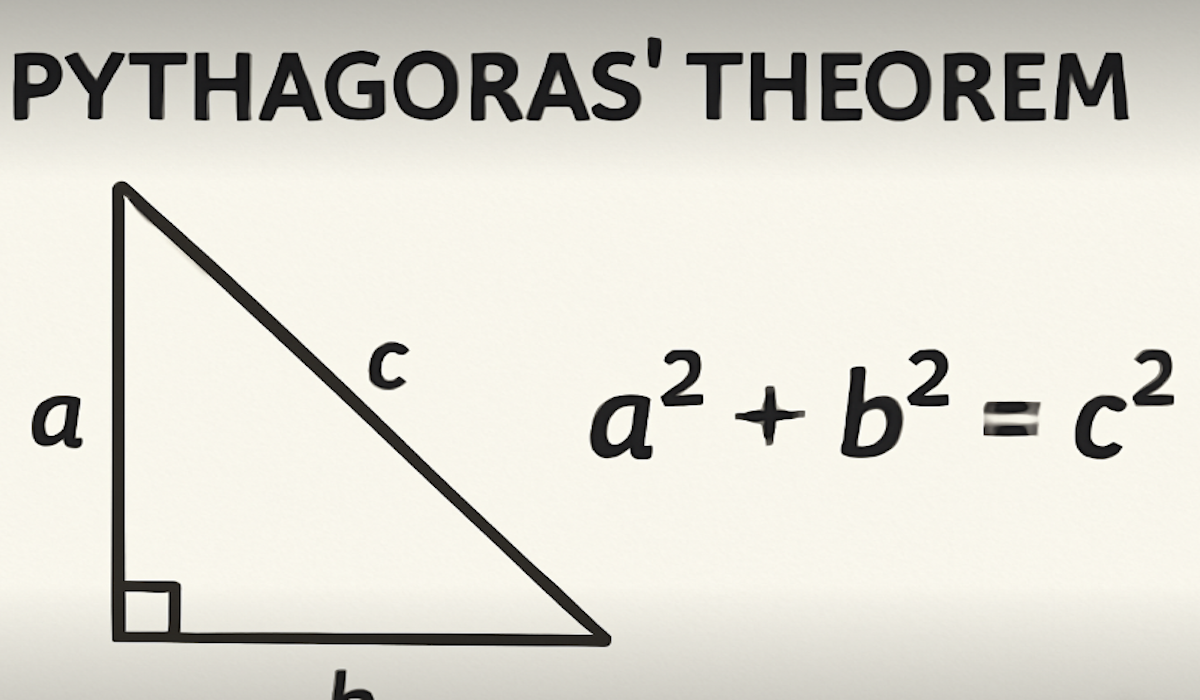Rumus Pythagoras: Menghitung Segitiga Siku-siku

Rumus Pythagoras(Ilustrasi: AI)

Dalam dunia matematika, terdapat sebuah konsep fundamental yang telah menjadi landasan bagi berbagai perhitungan dan aplikasi praktis, yaitu Teorema Pythagoras. Teorema ini, yang berkaitan erat dengan segitiga siku-siku, membuka pintu bagi pemahaman yang lebih mendalam tentang hubungan antara sisi-sisi segitiga dan memungkinkan kita untuk menghitung panjang sisi yang tidak diketahui dengan akurat. Mari kita selami lebih dalam mengenai keajaiban rumus Pythagoras ini.

Sejarah dan Asal Usul Teorema Pythagoras

Teorema Pythagoras, meskipun namanya mengacu pada seorang filsuf dan matematikawan Yunani kuno bernama Pythagoras, sebenarnya telah dikenal dan digunakan jauh sebelum zamannya. Bukti-bukti sejarah menunjukkan bahwa konsep dasar teorema ini telah dipahami oleh peradaban-peradaban kuno seperti Babilonia dan Mesir, yang menggunakannya dalam perhitungan praktis seperti pembangunan piramida dan pengukuran lahan.

Namun, Pythagoras dan para pengikutnya diyakini sebagai pihak yang pertama kali memberikan bukti formal dan sistematis mengenai teorema ini, sehingga namanya kemudian diabadikan sebagai penghormatan atas kontribusinya.

Pythagoras, yang hidup sekitar abad ke-6 SM, mendirikan sebuah sekolah filsafat dan matematika di Croton, Italia Selatan. Sekolah ini, yang dikenal sebagai Persaudaraan Pythagorean, memiliki minat yang mendalam terhadap angka dan geometri, dan mereka percaya bahwa angka adalah kunci untuk memahami alam semesta. Melalui penelitian dan eksplorasi mereka, para Pythagorean berhasil membuktikan berbagai teorema matematika, termasuk Teorema Pythagoras yang terkenal.

Meskipun bukti pasti mengenai bagaimana Pythagoras dan para pengikutnya menemukan dan membuktikan teorema ini masih menjadi misteri, terdapat beberapa teori yang menarik. Salah satu teori menyebutkan bahwa mereka mungkin telah menemukan teorema ini melalui pengamatan pola-pola geometris pada ubin atau lantai. Teori lain menyatakan bahwa mereka mungkin telah menggunakan metode eksperimen dan manipulasi fisik untuk memverifikasi kebenaran teorema ini.

Terlepas dari bagaimana teorema ini ditemukan, yang pasti adalah bahwa Teorema Pythagoras telah menjadi salah satu teorema matematika yang paling penting dan berpengaruh dalam sejarah. Teorema ini tidak hanya memberikan dasar bagi berbagai perhitungan geometris, tetapi juga memiliki aplikasi yang luas dalam berbagai bidang ilmu pengetahuan dan teknologi.

Memahami Konsep Dasar Segitiga Siku-Siku

Sebelum kita membahas lebih jauh mengenai Teorema Pythagoras, penting untuk memahami konsep dasar segitiga siku-siku. Segitiga siku-siku adalah segitiga yang memiliki satu sudut yang berukuran 90 derajat, yang disebut sudut siku-siku. Sisi yang berhadapan dengan sudut siku-siku disebut hipotenusa, yang merupakan sisi terpanjang dalam segitiga siku-siku. Dua sisi lainnya disebut kaki-kaki segitiga, yang membentuk sudut siku-siku.

Dalam Teorema Pythagoras, hubungan antara sisi-sisi segitiga siku-siku dinyatakan sebagai berikut: kuadrat panjang hipotenusa sama dengan jumlah kuadrat panjang kedua kaki segitiga. Secara matematis, teorema ini dapat ditulis sebagai:

a² + b² = c²

di mana:

• a dan b adalah panjang kaki-kaki segitiga
• c adalah panjang hipotenusa

Rumus ini memungkinkan kita untuk menghitung panjang salah satu sisi segitiga siku-siku jika kita mengetahui panjang dua sisi lainnya. Misalnya, jika kita mengetahui panjang kaki-kaki segitiga (a dan b), kita dapat menghitung panjang hipotenusa (c) dengan menggunakan rumus:

c = √(a² + b²)

Sebaliknya, jika kita mengetahui panjang hipotenusa (c) dan salah satu kaki segitiga (misalnya, a), kita dapat menghitung panjang kaki segitiga yang lain (b) dengan menggunakan rumus:

b = √(c² - a²)

Aplikasi Praktis Teorema Pythagoras dalam Kehidupan Sehari-hari

Teorema Pythagoras bukan hanya sekadar rumus matematika abstrak, tetapi juga memiliki aplikasi praktis yang luas dalam kehidupan sehari-hari. Berikut adalah beberapa contoh bagaimana teorema ini dapat digunakan:

• Konstruksi Bangunan: Dalam konstruksi bangunan, Teorema Pythagoras digunakan untuk memastikan bahwa sudut-sudut bangunan benar-benar siku-siku. Para tukang bangunan menggunakan teorema ini untuk mengukur dan memotong kayu, memasang ubin, dan membangun fondasi yang kokoh.
• Navigasi: Dalam navigasi, Teorema Pythagoras digunakan untuk menghitung jarak antara dua titik. Misalnya, seorang pelaut dapat menggunakan teorema ini untuk menghitung jarak antara kapal mereka dan pelabuhan tujuan.
• Desain Grafis: Dalam desain grafis, Teorema Pythagoras digunakan untuk membuat gambar dan animasi yang presisi. Para desainer grafis menggunakan teorema ini untuk menghitung panjang garis, sudut, dan jarak dalam desain mereka.
• Pemetaan: Dalam pemetaan, Teorema Pythagoras digunakan untuk menghitung jarak dan luas wilayah. Para pemeta menggunakan teorema ini untuk membuat peta yang akurat dan informatif.
• Olahraga: Dalam olahraga, Teorema Pythagoras digunakan untuk menghitung jarak dan sudut dalam berbagai aktivitas. Misalnya, seorang pemain bisbol dapat menggunakan teorema ini untuk menghitung jarak yang harus ditempuh bola untuk mencapai base.

Selain contoh-contoh di atas, Teorema Pythagoras juga digunakan dalam berbagai bidang ilmu pengetahuan dan teknologi lainnya, seperti fisika, teknik, dan astronomi. Teorema ini merupakan alat yang sangat berguna untuk memecahkan masalah-masalah yang melibatkan segitiga siku-siku dan hubungan antara sisi-sisinya.

Contoh Soal dan Pembahasan Teorema Pythagoras

Untuk lebih memahami bagaimana Teorema Pythagoras digunakan dalam praktik, mari kita bahas beberapa contoh soal:

Soal 1: Sebuah segitiga siku-siku memiliki kaki-kaki dengan panjang 3 cm dan 4 cm. Hitunglah panjang hipotenusa segitiga tersebut.

Pembahasan:

Kita dapat menggunakan rumus Teorema Pythagoras untuk menghitung panjang hipotenusa (c):

c = √(a² + b²)

Di mana a = 3 cm dan b = 4 cm.

c = √(3² + 4²)

c = √(9 + 16)

c = √25

c = 5 cm

Jadi, panjang hipotenusa segitiga tersebut adalah 5 cm.

Soal 2: Sebuah tangga dengan panjang 5 meter disandarkan pada dinding. Jarak antara kaki tangga dan dinding adalah 3 meter. Hitunglah tinggi dinding yang dicapai oleh tangga.

Pembahasan:

Dalam kasus ini, tangga, dinding, dan tanah membentuk sebuah segitiga siku-siku. Tangga adalah hipotenusa (c = 5 meter), jarak antara kaki tangga dan dinding adalah salah satu kaki segitiga (a = 3 meter), dan tinggi dinding yang dicapai oleh tangga adalah kaki segitiga yang lain (b).

Kita dapat menggunakan rumus Teorema Pythagoras untuk menghitung tinggi dinding (b):

b = √(c² - a²)

b = √(5² - 3²)

b = √(25 - 9)

b = √16

b = 4 meter

Jadi, tinggi dinding yang dicapai oleh tangga adalah 4 meter.

Soal 3: Sebuah kapal berlayar ke arah timur sejauh 12 km, kemudian berbelok ke arah utara sejauh 5 km. Hitunglah jarak terpendek antara posisi awal kapal dan posisi akhirnya.

Pembahasan:

Pergerakan kapal membentuk dua sisi dari sebuah segitiga siku-siku. Jarak ke arah timur adalah salah satu kaki segitiga (a = 12 km), jarak ke arah utara adalah kaki segitiga yang lain (b = 5 km), dan jarak terpendek antara posisi awal dan posisi akhir kapal adalah hipotenusa (c).

Kita dapat menggunakan rumus Teorema Pythagoras untuk menghitung jarak terpendek (c):

c = √(a² + b²)

c = √(12² + 5²)

c = √(144 + 25)

c = √169

c = 13 km

Jadi, jarak terpendek antara posisi awal kapal dan posisi akhirnya adalah 13 km.

Triple Pythagoras: Kombinasi Angka yang Istimewa

Dalam Teorema Pythagoras, terdapat beberapa kombinasi angka yang memenuhi persamaan a² + b² = c² dengan a, b, dan c adalah bilangan bulat positif. Kombinasi angka seperti ini disebut Triple Pythagoras. Contoh Triple Pythagoras yang paling terkenal adalah (3, 4, 5), karena 3² + 4² = 5² (9 + 16 = 25).

Triple Pythagoras memiliki beberapa sifat menarik. Salah satunya adalah bahwa jika (a, b, c) adalah Triple Pythagoras, maka (ka, kb, kc) juga merupakan Triple Pythagoras untuk setiap bilangan bulat positif k. Misalnya, karena (3, 4, 5) adalah Triple Pythagoras, maka (6, 8, 10), (9, 12, 15), dan seterusnya juga merupakan Triple Pythagoras.

Selain (3, 4, 5), terdapat banyak Triple Pythagoras lainnya, seperti (5, 12, 13), (8, 15, 17), (7, 24, 25), dan seterusnya. Triple Pythagoras sering digunakan dalam soal-soal matematika dan memiliki aplikasi praktis dalam berbagai bidang, seperti konstruksi dan navigasi.

Berikut adalah beberapa contoh Triple Pythagoras:

a b c

3	4	5
5	12	13
8	15	17
7	24	25
20	21	29

Bukti-Bukti Teorema Pythagoras

Selama berabad-abad, banyak matematikawan telah memberikan bukti-bukti yang berbeda mengenai Teorema Pythagoras. Beberapa bukti menggunakan pendekatan geometris, sementara yang lain menggunakan pendekatan aljabar. Berikut adalah beberapa contoh bukti Teorema Pythagoras:

• Bukti Geometris dengan Luas Persegi: Bukti ini melibatkan pembentukan dua persegi yang sama besar. Pada persegi pertama, kita menempatkan empat segitiga siku-siku yang identik di sudut-sudutnya, sehingga membentuk sebuah persegi kecil di tengahnya. Pada persegi kedua, kita menempatkan empat segitiga siku-siku yang sama dengan cara yang berbeda, sehingga membentuk dua persegi yang lebih kecil di tengahnya. Dengan membandingkan luas kedua persegi tersebut, kita dapat membuktikan Teorema Pythagoras.
• Bukti Aljabar dengan Manipulasi Persamaan: Bukti ini melibatkan manipulasi persamaan aljabar untuk menunjukkan bahwa a² + b² = c². Kita mulai dengan membentuk sebuah persegi dengan sisi (a + b). Luas persegi ini adalah (a + b)². Kemudian, kita membagi persegi ini menjadi empat segitiga siku-siku yang identik dengan sisi a dan b, serta sebuah persegi dengan sisi c. Dengan menyamakan luas persegi besar dengan jumlah luas keempat segitiga dan persegi kecil, kita dapat membuktikan Teorema Pythagoras.
• Bukti dengan Kesebangunan Segitiga: Bukti ini melibatkan penggunaan konsep kesebangunan segitiga. Kita menggambar garis tinggi dari sudut siku-siku segitiga siku-siku ke hipotenusa. Garis tinggi ini membagi segitiga siku-siku menjadi dua segitiga yang lebih kecil, yang keduanya sebangun dengan segitiga siku-siku awal. Dengan menggunakan perbandingan sisi-sisi yang bersesuaian pada segitiga-segitiga yang sebangun, kita dapat membuktikan Teorema Pythagoras.

Bukti-bukti ini menunjukkan bahwa Teorema Pythagoras adalah sebuah teorema yang kokoh dan memiliki dasar yang kuat dalam matematika.

Generalisasi Teorema Pythagoras: Hukum Cosinus

Teorema Pythagoras hanya berlaku untuk segitiga siku-siku. Namun, terdapat sebuah generalisasi dari teorema ini yang berlaku untuk semua jenis segitiga, yaitu Hukum Cosinus. Hukum Cosinus menyatakan bahwa kuadrat panjang salah satu sisi segitiga sama dengan jumlah kuadrat panjang kedua sisi lainnya dikurangi dua kali hasil kali panjang kedua sisi tersebut dengan cosinus sudut yang diapit oleh kedua sisi tersebut.

Secara matematis, Hukum Cosinus dapat ditulis sebagai:

c² = a² + b² - 2ab cos(C)

di mana:

• a, b, dan c adalah panjang sisi-sisi segitiga
• C adalah sudut yang diapit oleh sisi a dan b

Jika sudut C adalah sudut siku-siku (90 derajat), maka cos(C) = 0, dan Hukum Cosinus menjadi Teorema Pythagoras: c² = a² + b².

Hukum Cosinus sangat berguna untuk menghitung panjang sisi atau besar sudut pada segitiga sembarang, terutama ketika kita tidak memiliki informasi yang cukup untuk menggunakan Teorema Pythagoras atau fungsi trigonometri dasar.

Kesimpulan

Teorema Pythagoras adalah salah satu teorema matematika yang paling penting dan berpengaruh dalam sejarah. Teorema ini memberikan dasar bagi berbagai perhitungan geometris dan memiliki aplikasi yang luas dalam berbagai bidang ilmu pengetahuan dan teknologi.

Dari konstruksi bangunan hingga navigasi, dari desain grafis hingga olahraga, Teorema Pythagoras telah membuktikan dirinya sebagai alat yang sangat berguna untuk memecahkan masalah-masalah yang melibatkan segitiga siku-siku dan hubungan antara sisi-sisinya.

Dengan memahami konsep dasar dan aplikasi praktis Teorema Pythagoras, kita dapat meningkatkan kemampuan kita dalam memecahkan masalah dan memahami dunia di sekitar kita dengan lebih baik. (Z-10)