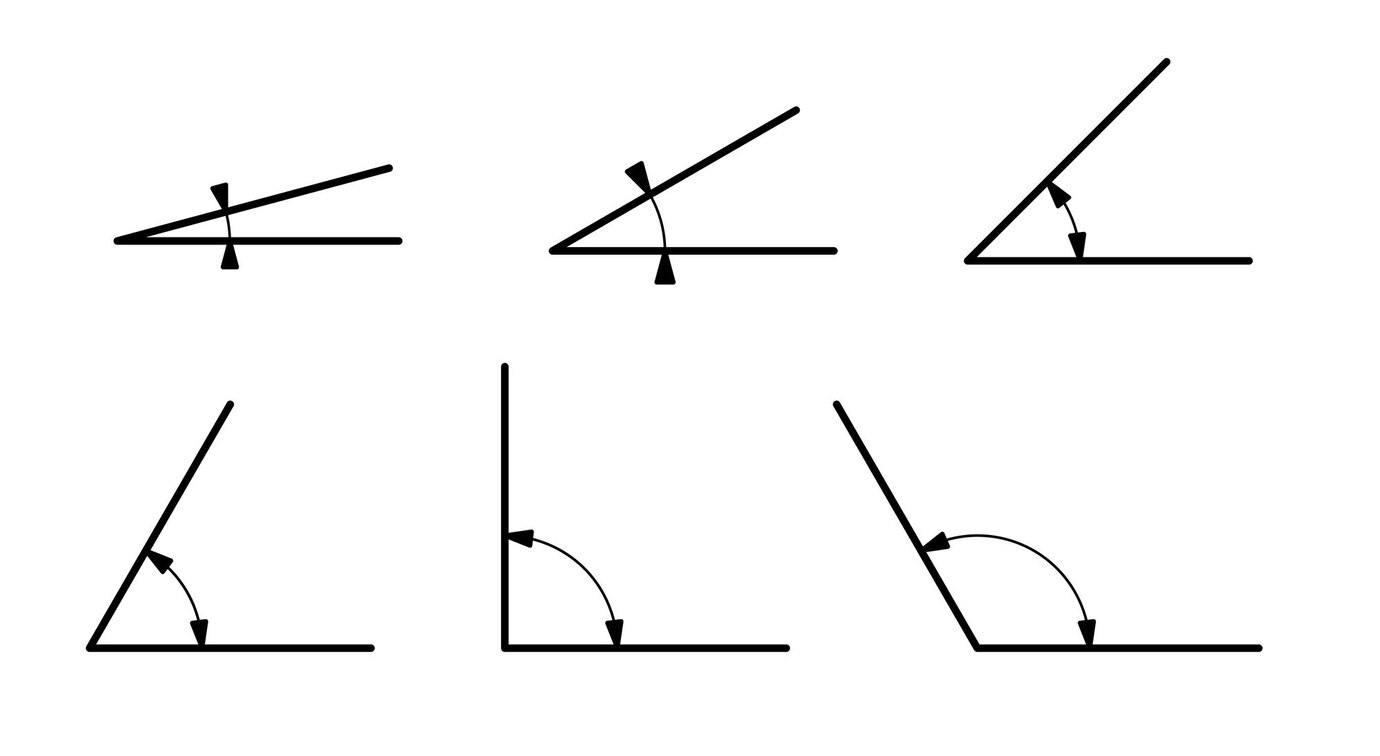6 days ago
15
Ilustrasi(freepik.com)
DALAM dunia matematika, khususnya geometri, sudut memegang peranan krusial sebagai fondasi untuk memahami bentuk dan ruang. Sudut, yang terbentuk dari dua garis yang bertemu pada satu titik, bukan hanya sekadar elemen visual, melainkan juga kunci untuk mengukur dan menganalisis hubungan antar objek dalam berbagai dimensi. Pemahaman mendalam tentang berbagai jenis sudut membuka pintu menuju pemecahan masalah yang kompleks, mulai dari navigasi hingga desain arsitektur. Mari kita selami lebih dalam tentang ragam sudut dan bagaimana mereka berperan dalam kehidupan sehari-hari.
Jenis-Jenis Sudut dan Karakteristiknya
Sudut diklasifikasikan berdasarkan ukurannya, yang diukur dalam derajat (°). Setiap jenis sudut memiliki karakteristik unik yang membedakannya dari yang lain. Berikut adalah beberapa jenis sudut yang paling umum:
Sudut Lancip: Sudut lancip adalah sudut yang ukurannya lebih dari 0° dan kurang dari 90°. Bentuknya yang lancip membuatnya mudah dikenali. Sudut ini sering ditemukan dalam desain modern, memberikan kesan dinamis dan tajam.
Sudut Siku-Siku: Sudut siku-siku adalah sudut yang ukurannya tepat 90°. Sudut ini sangat penting dalam geometri karena menjadi dasar untuk banyak bentuk dan konstruksi. Simbol sudut siku-siku adalah kotak kecil di titik pertemuan kedua garis.
Sudut Tumpul: Sudut tumpul adalah sudut yang ukurannya lebih dari 90° dan kurang dari 180°. Bentuknya yang terbuka memberikan kesan luas dan nyaman. Sudut ini sering digunakan dalam desain interior untuk menciptakan ruang yang terasa lebih besar.
Sudut Lurus: Sudut lurus adalah sudut yang ukurannya tepat 180°. Sudut ini membentuk garis lurus. Sudut lurus sering digunakan sebagai referensi dalam pengukuran sudut lainnya.
Sudut Refleks: Sudut refleks adalah sudut yang ukurannya lebih dari 180° dan kurang dari 360°. Sudut ini melampaui garis lurus dan mengarah kembali ke titik awal.
Sudut Penuh: Sudut penuh adalah sudut yang ukurannya tepat 360°. Sudut ini membentuk lingkaran penuh.
Selain jenis-jenis sudut di atas, terdapat juga beberapa istilah lain yang berkaitan dengan sudut, seperti sudut komplemen dan sudut suplemen.
Sudut Komplemen: Dua sudut dikatakan komplemen jika jumlah ukurannya adalah 90°. Misalnya, sudut 30° dan sudut 60° adalah sudut komplemen.
Sudut Suplemen: Dua sudut dikatakan suplemen jika jumlah ukurannya adalah 180°. Misalnya, sudut 120° dan sudut 60° adalah sudut suplemen.
Penerapan Sudut dalam Kehidupan Sehari-hari
Sudut bukan hanya konsep abstrak dalam matematika, tetapi juga memiliki penerapan yang luas dalam kehidupan sehari-hari. Berikut adalah beberapa contoh penerapan sudut dalam berbagai bidang:
Arsitektur: Sudut sangat penting dalam desain dan konstruksi bangunan. Sudut yang tepat memastikan stabilitas dan estetika bangunan. Misalnya, sudut siku-siku digunakan untuk membuat dinding yang tegak lurus, sedangkan sudut lancip dan tumpul digunakan untuk menciptakan desain yang unik dan menarik.
Navigasi: Sudut digunakan dalam navigasi untuk menentukan arah dan posisi. Kompas menggunakan sudut untuk menunjukkan arah mata angin, sedangkan GPS menggunakan sudut untuk menghitung koordinat lokasi.
Teknologi: Sudut digunakan dalam berbagai perangkat teknologi, seperti kamera, layar, dan sensor. Sudut pandang kamera menentukan seberapa luas area yang dapat ditangkap, sedangkan sudut kemiringan layar menentukan kenyamanan pengguna.
Seni dan Desain: Sudut digunakan dalam seni dan desain untuk menciptakan komposisi yang menarik dan seimbang. Sudut pandang yang berbeda dapat memberikan kesan yang berbeda pada sebuah karya seni.
Olahraga: Sudut digunakan dalam berbagai olahraga, seperti sepak bola, basket, dan golf. Sudut tembakan menentukan arah dan jarak bola, sedangkan sudut ayunan menentukan kekuatan dan akurasi pukulan.
Mengukur Sudut dengan Alat yang Tepat
Pengukuran sudut yang akurat sangat penting dalam berbagai aplikasi. Terdapat beberapa alat yang dapat digunakan untuk mengukur sudut, di antaranya:
Busur Derajat: Busur derajat adalah alat yang paling umum digunakan untuk mengukur sudut. Alat ini berbentuk setengah lingkaran dengan skala derajat dari 0° hingga 180°. Untuk mengukur sudut, letakkan titik tengah busur derajat pada titik pertemuan kedua garis, lalu baca angka pada skala yang sejajar dengan garis kedua.
Teodolit: Teodolit adalah alat yang digunakan untuk mengukur sudut horizontal dan vertikal. Alat ini sering digunakan dalam survei tanah dan konstruksi bangunan.
Klinometer: Klinometer adalah alat yang digunakan untuk mengukur sudut kemiringan atau elevasi. Alat ini sering digunakan dalam geologi dan kehutanan.
Sensor Sudut: Sensor sudut adalah perangkat elektronik yang digunakan untuk mengukur sudut secara otomatis. Sensor ini sering digunakan dalam robotika dan otomasi.
Hubungan Antar Sudut dalam Geometri
Dalam geometri, sudut seringkali berhubungan satu sama lain. Memahami hubungan antar sudut dapat membantu dalam memecahkan masalah geometri yang kompleks. Berikut adalah beberapa hubungan antar sudut yang penting:
Sudut Sehadap: Dua sudut dikatakan sehadap jika terletak pada posisi yang sama pada dua garis sejajar yang dipotong oleh garis transversal. Sudut sehadap memiliki ukuran yang sama.
Sudut Dalam Berseberangan: Dua sudut dikatakan dalam berseberangan jika terletak di antara dua garis sejajar dan berada di sisi yang berlawanan dari garis transversal. Sudut dalam berseberangan memiliki ukuran yang sama.
Sudut Luar Berseberangan: Dua sudut dikatakan luar berseberangan jika terletak di luar dua garis sejajar dan berada di sisi yang berlawanan dari garis transversal. Sudut luar berseberangan memiliki ukuran yang sama.
Sudut Dalam Sepihak: Dua sudut dikatakan dalam sepihak jika terletak di antara dua garis sejajar dan berada di sisi yang sama dari garis transversal. Jumlah ukuran sudut dalam sepihak adalah 180°.
Sudut Luar Sepihak: Dua sudut dikatakan luar sepihak jika terletak di luar dua garis sejajar dan berada di sisi yang sama dari garis transversal. Jumlah ukuran sudut luar sepihak adalah 180°.
Tips dan Trik dalam Memahami Sudut
Memahami sudut membutuhkan latihan dan pemahaman konsep yang kuat. Berikut adalah beberapa tips dan trik yang dapat membantu dalam memahami sudut:
Visualisasikan Sudut: Bayangkan sudut sebagai bukaan antara dua garis. Semakin besar bukaannya, semakin besar pula ukuran sudutnya.
Gunakan Alat Bantu: Gunakan busur derajat atau alat pengukur sudut lainnya untuk membantu memvisualisasikan dan mengukur sudut.
Latihan Soal: Kerjakan soal-soal latihan yang beragam untuk menguji pemahaman tentang sudut.
Cari Contoh di Kehidupan Nyata: Perhatikan sudut-sudut di sekitar Anda, seperti sudut dinding, sudut meja, atau sudut atap rumah.
Gunakan Sumber Belajar yang Tepat: Gunakan buku, video, atau sumber belajar online yang terpercaya untuk memperdalam pemahaman tentang sudut.
Peran Sudut dalam Trigonometri
Sudut memegang peranan sentral dalam trigonometri, cabang matematika yang mempelajari hubungan antara sudut dan sisi-sisi segitiga. Fungsi trigonometri, seperti sinus (sin), kosinus (cos), dan tangen (tan), didefinisikan berdasarkan sudut dalam segitiga siku-siku. Fungsi-fungsi ini memungkinkan kita untuk menghitung panjang sisi segitiga jika kita mengetahui ukuran sudut dan panjang sisi lainnya, atau sebaliknya.
Trigonometri memiliki aplikasi yang luas dalam berbagai bidang, termasuk:
Navigasi: Menentukan posisi dan arah menggunakan sudut dan jarak.
Fisika: Menganalisis gerak proyektil, gelombang, dan gaya.
Teknik: Merancang struktur bangunan, jembatan, dan mesin.
Astronomi: Menentukan posisi bintang dan planet.
Sudut dalam Dimensi yang Lebih Tinggi
Konsep sudut tidak hanya terbatas pada bidang dua dimensi. Dalam ruang tiga dimensi, kita juga dapat mendefinisikan sudut antara dua bidang atau antara garis dan bidang. Sudut dihedral adalah sudut antara dua bidang yang berpotongan, sedangkan sudut antara garis dan bidang adalah sudut terkecil antara garis tersebut dan garis yang terletak pada bidang yang tegak lurus terhadap garis tersebut.
Pemahaman tentang sudut dalam dimensi yang lebih tinggi sangat penting dalam bidang-bidang seperti:
Grafika Komputer: Membuat model 3D dan animasi.
Kimia: Memahami struktur molekul.
Kedokteran: Menganalisis citra medis seperti CT scan dan MRI.
Sudut dan Simetri
Sudut memiliki hubungan erat dengan simetri. Sebuah objek dikatakan simetris jika memiliki bagian-bagian yang sama atau serupa yang tersusun secara teratur. Sudut seringkali menjadi elemen kunci dalam menentukan simetri suatu objek. Misalnya, sebuah persegi memiliki simetri rotasi 90°, yang berarti bahwa jika persegi tersebut diputar sebesar 90°, ia akan terlihat sama seperti semula.
Simetri dapat ditemukan dalam berbagai aspek kehidupan, mulai dari alam hingga seni dan desain. Pemahaman tentang sudut dan simetri membantu kita untuk mengapresiasi keindahan dan keteraturan dunia di sekitar kita.
Sudut dalam Seni dan Desain
Sudut memainkan peran penting dalam seni dan desain, baik dalam menciptakan komposisi yang menarik maupun dalam menyampaikan pesan tertentu. Sudut pandang yang berbeda dapat memberikan kesan yang berbeda pada sebuah karya seni. Misalnya, sudut pandang rendah dapat membuat objek terlihat lebih besar dan kuat, sedangkan sudut pandang tinggi dapat membuat objek terlihat lebih kecil dan lemah.
Selain itu, sudut juga dapat digunakan untuk menciptakan ilusi optik dan efek visual yang menarik. Misalnya, perspektif linear menggunakan sudut untuk menciptakan kesan kedalaman pada gambar dua dimensi.
Sudut dalam Musik
Meskipun terdengar tidak lazim, sudut juga memiliki hubungan dengan musik. Dalam teori musik, interval antara dua nada dapat diukur dalam derajat. Misalnya, interval antara nada C dan nada G adalah interval kelima, yang setara dengan sudut 72° pada lingkaran nada.
Selain itu, beberapa alat musik, seperti gitar dan biola, menggunakan sudut untuk mengatur tegangan senar dan menghasilkan nada yang berbeda. Sudut antara senar dan jembatan pada gitar, misalnya, mempengaruhi kualitas suara yang dihasilkan.
Kesimpulan
Sudut adalah konsep fundamental dalam matematika dan memiliki penerapan yang luas dalam berbagai bidang kehidupan. Dari arsitektur hingga navigasi, dari teknologi hingga seni dan desain, sudut memainkan peran penting dalam membentuk dunia di sekitar kita. Memahami berbagai jenis sudut, cara mengukurnya, dan hubungannya dengan konsep-konsep lain seperti trigonometri dan simetri adalah kunci untuk membuka pemahaman yang lebih dalam tentang dunia matematika dan aplikasinya.
Dengan terus berlatih dan mengeksplorasi konsep sudut, kita dapat mengembangkan kemampuan berpikir logis dan analitis yang sangat berharga dalam memecahkan masalah dan mengambil keputusan dalam berbagai aspek kehidupan.
Semoga artikel ini bermanfaat dan memberikan wawasan baru tentang dunia sudut yang menarik!
